26+ Wahrheiten in Gram Schmidt Verfahren Beispiel: Wir orthogonalisieren die vektoren a 1 … a 3 a = (a 1, a 2, a 3) = (0 8 10 2 4 6 0 0 12)
Gram Schmidt Verfahren Beispiel | Q~ j = ~q j r 3jq 3; Man de niert sukzessive u j = b j x k<j hu k;b ji hu k;u ki u k; Den ersten vektor \( v_1 \) übernimmst du einfach. Es geht um drei vektoren, die orthonomiert werden solln. Zunächst müssen wir den vektor normieren.
Mit dem verfahren kann nun ein orthogonalsystem von \( n \) paarweise orthogonalen vektoren berechnet werden, das denselben untervektorraum erzeugt. Es geht um drei vektoren, die orthonomiert werden solln. Das gram schmidtsches orthogonalisierungsverfahren ist eine methode zur konstruktion von orthonormalbasen. Das eben beschriebene verfahren soll uns nun zwei orthogonale vektoren liefern. Berechnen wir nun das produkt so erhalten wir eine obere dreiecksmatrix.

Nun orthogonalisieren wir den zweiten vektor: Wir orthogonalisieren die vektoren a 1 … a 3 a = (a 1, a 2, a 3) = (0 8 10 2 4 6 0 0 12) $$$ \mathbf{\vec{v_1}} $$$ $$$ \mathbf{\vec{v_2}} $$$ $$$ \mathbf{\vec{v_3}} $$$ if the calculator did not compute something or you have identified an error, or you have a suggestion/feedback, please write it in the comments below. Denn aufgrund der konstruktion der orthogonalen vektoren gilt für alle , dass. Es kursieren zwei mögliche algorithmen: Dazu betrachten wir die vektoren. Im versehen mit dem standardskalarprodukt seien zwei linear unabhängige vektoren vorgegeben, die einen untervektorraum erzeugen: Orthogonalisierungsverfahren gram schmidtsches essay beispiel. Für die einzelnen vektoren \( v_1, \dots, v_n \) gilt: Den ersten vektor \( v_1 \) übernimmst du einfach. Q~ j = ~q j r 3jq 3; R 3j = q t 3 q~ j usw. F ur j = 1;:::;n.
Er erzeugt zu jedem system linear unabhängiger vektoren aus einem prähilbertraum (einem vektorraum mit skalarprodukt ) ein orthogonalsystem , das denselben untervektorraum erzeugt. Gram schmidt orthonormalisierungsverfahren schmidtsches orthonormalisierungsverfahren beispiel. Das gram schmidtsches orthogonalisierungsverfahren ist eine methode zur konstruktion von orthonormalbasen. Für die einzelnen vektoren \( v_1, \dots, v_n \) gilt: Dazu betrachten wir die linear unabhängigen vektoren.
Es kursieren zwei mögliche algorithmen: Dabei ist die summe die orthogonale projektion von b j auf span(u 1;:::;u j 1). Q~ j = ~q j r 3jq 3; Was deutlich dichter an der einheitsmatrix dran liegt. Q~ j = a j r 1jq 1; Den zweiten vektor berechnen wir gemäß des algorithmuses wie folgt. Dazu betrachten wir die vektoren. Es geht um drei vektoren, die orthonomiert werden solln. Berechnen wir nun das produkt so erhalten wir eine obere dreiecksmatrix. Das gram schmidtsches orthogonalisierungsverfahren ist eine methode zur konstruktion von orthonormalbasen. Wir wollen die idee des gram schmidt verfahrens an einem kurzen beispiel noch einmal demonstrieren. Im ersten rechenschritt veränderst du den vektor \( v_2 \) so, dass er orthogonal zum ersten vektor steht. Orthogonalisierungsverfahren gram schmidtsches essay beispiel.
Berechnen wir nun das produkt so erhalten wir eine obere dreiecksmatrix. R 1j = q t 1 a j anschlieˇend orthogonalisiere~q j gegen q 2: F ur j = 1;:::;n. Die rekursion vereinfacht sich, wenn man die basisvektoren nach jedem schritt normiert: Was deutlich dichter an der einheitsmatrix dran liegt.
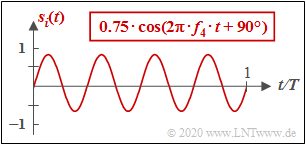
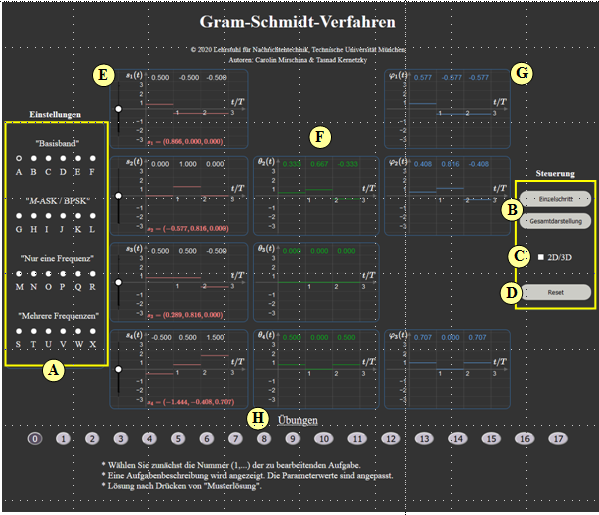
R 1j = q t 1 a j anschlieˇend orthogonalisiere~q j gegen q 2: Berechnen wir nun das produkt so erhalten wir eine obere dreiecksmatrix. Im dritten schritt versuchst du jetzt den dritten vektor orthogonal zu den. Er enthält einen link zu einer simulation zur konstruktion einer orthonormierten basis im r 3. Im letzten $\text{beispiel}$ war die bestimmung der beiden orthonormalen basisfunktionen $\varphi_1(t)$ und $\varphi_2(t)$ sehr einfach, da diese formgleich mit $s_1(t)$ bzw. Es geht um drei vektoren, die orthonomiert werden solln. Für die einzelnen vektoren \( v_1, \dots, v_n \) gilt: Die rekursion vereinfacht sich, wenn man die basisvektoren nach jedem schritt normiert: Der folgende algorithmus berechnet zu den linear unabhängigen vektoren ein orthonormalsystem von n normi Wir orthogonalisieren die vektoren a 1 … a 3 a = (a 1, a 2, a 3) = (0 8 10 2 4 6 0 0 12) F olgende v ektoren des r 3: Orthogonalisierungsverfahren gram schmidtsches essay beispiel. Die folgende funktion gramschmidt übernimmt als parameter einen verweis auf eine matrix b, deren zeilen die basisvektoren sind.
Gram Schmidt Verfahren Beispiel: R 3j = q t 3 q~ j usw.
Comments
Post a Comment